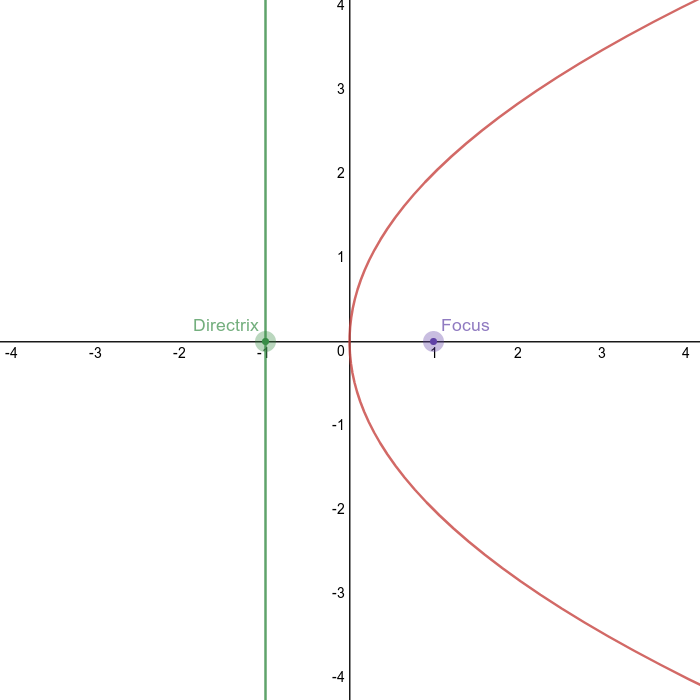
Parabola ($y^2$)
Definition: the set of points equidistant from the focus (point) and the directrix (line).
Equation: $y^2 = 4px$
Dominant Axis: $x$-axis
How to tell: The $x$ variable is linear
Vertex: $(0,0)$
Focus: $(p,0)$
Directrix: $x=-p$
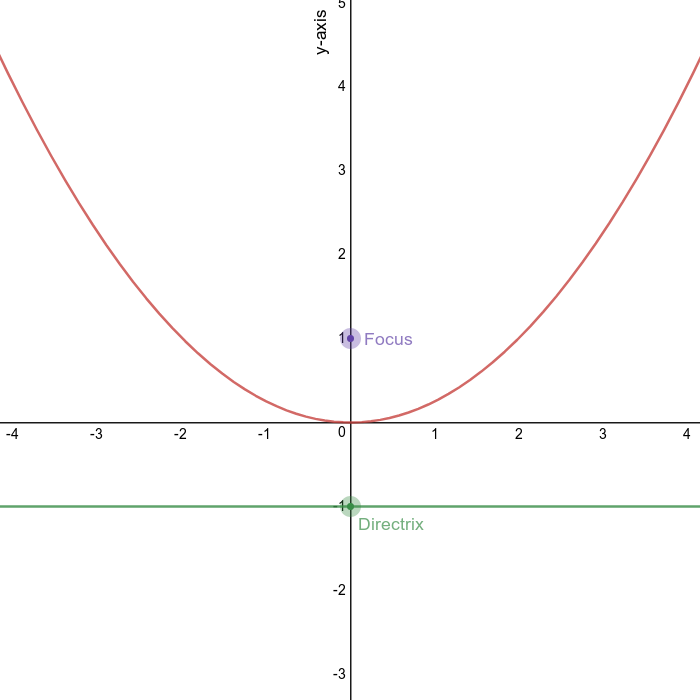
Parabola ($x^2$)
Definition: the set of points equidistant from the focus (point) and the directrix (line).
Equation: $x^2 = 4py$
Dominant Axis: $y$-axis
How to tell: The $y$ variable is linear
Vertex: $(0,0)$
Focus: $(0,p)$
Directrix: $y=-p$
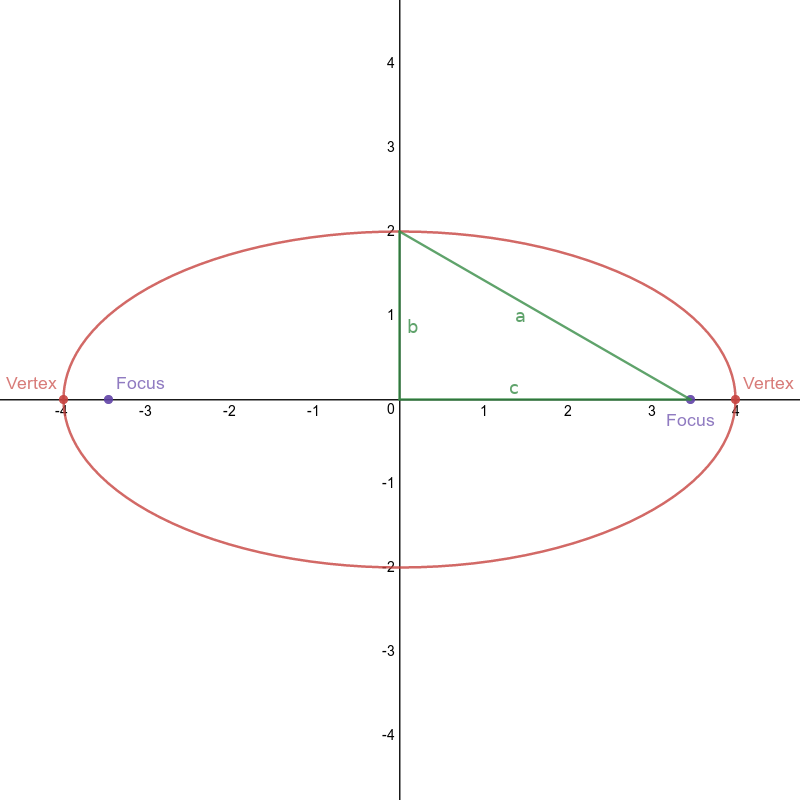
Ellipse (major $x$-axis)
Definition: the set of points whose sum of distances to two other fixed points (foci) is constant.
Equation: $\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$
Dominant Axis: $x$-axis
How to tell: The denominator for $x^2$ is larger
Center: $(0,0)$
Vertices: $(\pm a,0)$
Foci: $(\pm c,0)$ where $b^2+c^2 = a^2$
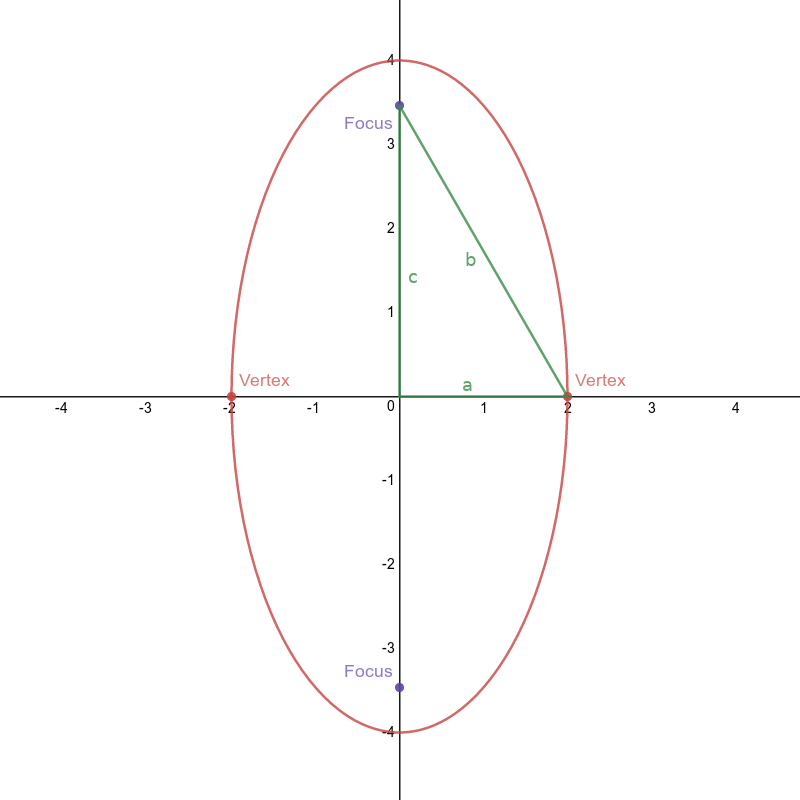
Ellipse (major $y$-axis)
Definition: the set of points whose sum of distances to two other fixed points (foci) is constant.
Equation: $\frac{y^2}{a^2}+\frac{x^2}{b^2} = 1$
Dominant Axis: $y$-axis
How to tell: The denominator for $y^2$ is larger
Center: $(0,0)$
Vertices: $(0,\pm a)$
Foci: $(0,\pm c)$ where $b^2+c^2 = a^2$
Hyperbola
(opens along $x$-axis)
Definition: the set of points whose difference of distances to two other fixed points (foci) is constant.
Equation: $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$
Dominant Axis: $x$-axis
How to tell: The $x^2$ is positive
Center: $(0,0)$
Vertices: $(\pm a, 0)$
Foci: $(\pm c, 0)$ where $a^2+b^2 = c^2$
Asymptotes: $y=\pm \frac{b}{a}x$
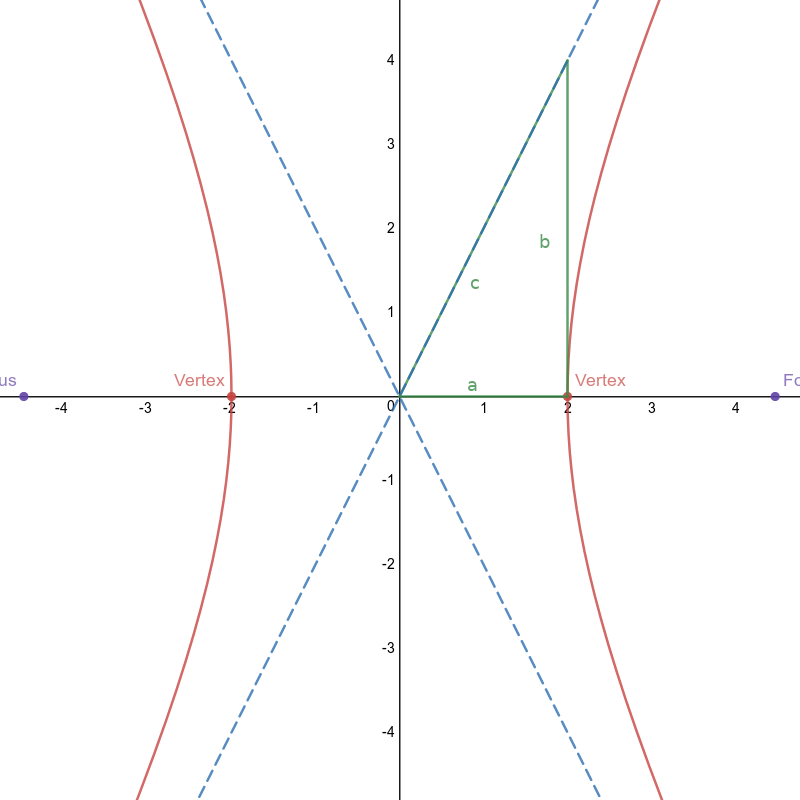
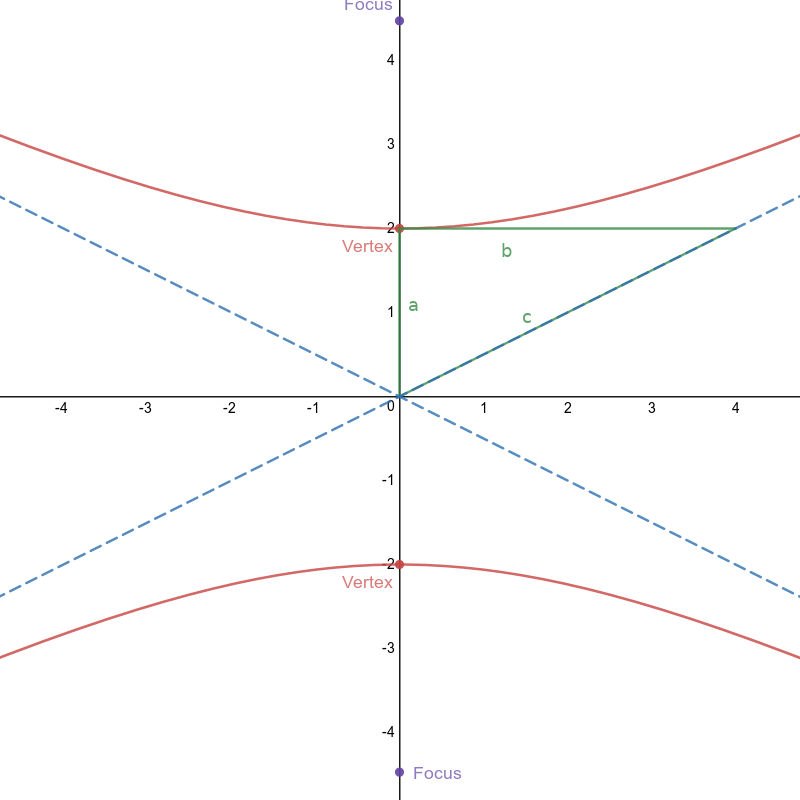
Hyperbola
(opens along $y$-axis)
Definition: the set of points whose difference of distances to two other fixed points (foci) is constant.
Equation: $\frac{y^2}{a^2}-\frac{x^2}{b^2} = 1$
Dominant Axis: $y$-axis
How to tell: The $y^2$ is positive
Center: $(0,0)$
Vertices: $(0, \pm a)$
Foci: $(0, \pm c)$ where $a^2+b^2 = c^2$
Asymptotes: $y=\pm \frac{a}{b}x$