Abstract

Center of Mass of a Cylinder as it is “drilled out”

by Dave Melvin, Andrew Knudson, Ben Humburg, Sierra College (A part of Honors Contract for Math 32 Fall 2011)

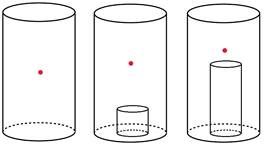
Consider a right circular cylinder of radius b and height h (oriented vertically where the origin is at the center of the base). It is a rudimentary calculation to show the center of mass is at the coordinate . Now consider drilling out (from the bottom) a cylinder of radius a (where a<b). As material is removed from the bottom of the cylinder, the center of mass (as expected) moves up. Now fast forward to when the cylinder has been completely drilled out. 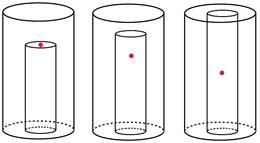Again it is a rudimentary calculation to show the center of mass is NOW BACK at the coordinate . The purpose of this talk is to use techniques of triple integrals (studied in Math 32) to determine this maximum “location” of this moving center of mass.